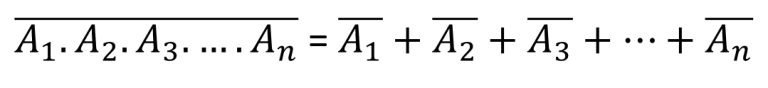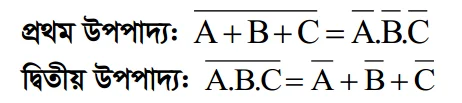ডি মরগ্যানের উপপাদ্য | সত্যক সারণি (De Morgan’s Theorem)
ফরাসি গণিতবিদ ডি মরগ্যান, বুলিয়ান ফাংশন সরলীকরণ করার জন্য দুটি সূত্র আবিষ্কার করেন।
প্রথম উপপাদ্যঃ যেকোন সংখ্যক চলকের যৌক্তিক যোগের পূরক বা কমপ্লিমেন্ট , প্রত্যেক চলকের পূরক বা কমপ্লিমেন্টের যৌক্তিক গুণের সমান। n সংখ্যক চলকের জন্য প্রথম উপপাদ্য-
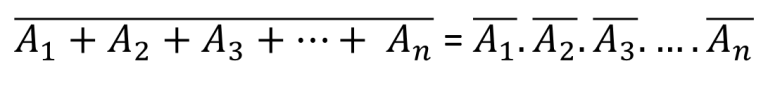দ্বিতীয় উপপাদ্যঃ যেকোন সংখ্যক চলকের যৌক্তিক গুণের পূরক বা কমপ্লিমেন্ট, প্রত্যেক চলকের পূরক বা কমপ্লিমেন্টের যৌক্তিক যোগের সমান। n সংখ্যক চলকের জন্য দ্বিতীয় উপপাদ্য –
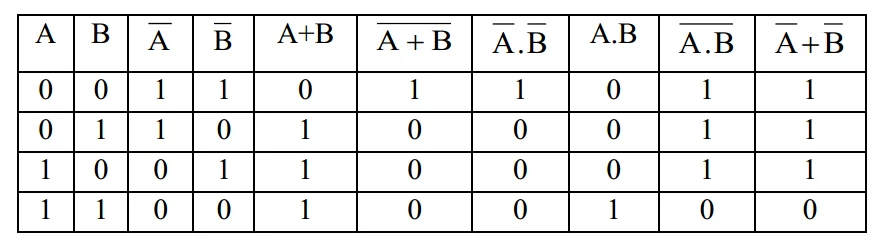
A ও B দুটি চলকের জন্য ডি-মরগ্যানের উপপাদ্য দুটি নিম্নরূপ−
A ,B ও C তিনটি চলকের জন্য ডি-মরগ্যানের উপপাদ্য দুটি নিম্নরূপ−
সত্যক সারণি কী?
যে সারণির মাধ্যমে বুলিয়ান সমীকরণে চলকসমূহের বিভিন্ন মানবিন্যাসের জন্য বিভিন্ন আউটপুট প্রদর্শন করা হয়, তাকে সত্যক সারণি বলে। সত্যক সারণির সাহায্যে বুলিয়ান সমীকরণের সত্যতা যাচাই করা হয়।
যদি বুলিয়ান সমীকরণে n সংখ্যক চলক থাকে, তবে সত্যক সারণিতে ইনপুট কম্বিনেশন হবে 2n সংখ্যক এবং আউটপুটও হবে 2n সংখ্যক।
উদাহরনঃ একটি অর(OR) লজিক গেইটের ইনপুট চলক A ও B এর সাপেক্ষে আউটপুট ফাংশন F= A+B এর সত্যক সারণি দেখানো হল। যেহেতু চলক দুইটি (A ও B) তাই ইনপুট সেট ২২=৪ টি হবে।
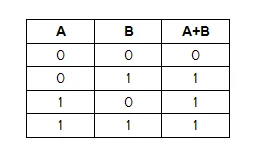
সত্যক সারণি থেকে আউটপুটের বুলিয়ান এক্সপ্রেশন বা সমীকরণ লেখার উপায়ঃ
সত্যক সারণির বুলিয়ান ফাংশন দুই ভাবে নির্ণয় করা যায়। যথা-
- মিনটার্মের সাহায্যে
- ম্যাক্সটার্মের সাহায্যে
মিনটার্মের সাহায্যে সারণির বুলিয়ান ফাংশন নির্ণয়ঃ
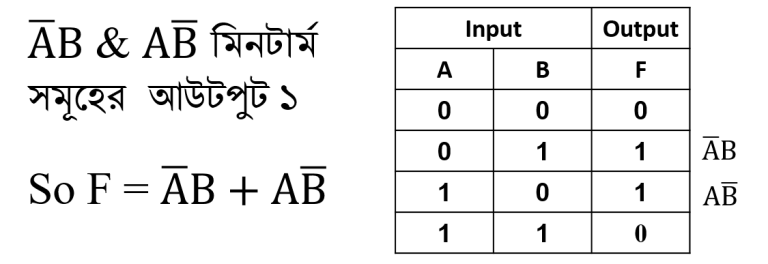
সত্যক সারণিতে ব্যবহৃত ইনপুট বিন্যাসসমূহের গুণফলকে বলা হয় মিনটার্ম। প্রতিটি মিনটার্মের মান ১ হয়। সত্যক সারণির যেসব মিনটার্মের আউটপুট মান ১, সেই মিনটার্মসমূহ যোগ করে বুলিয়ান ফাংশন নির্ণয় করা হয়। এ পদ্ধতিকে SOP(Sum of Products) বলা হয়।
ম্যাক্সটার্মের সাহায্যে সারণির আউটপুট ফাংশন নির্ণয়ঃ
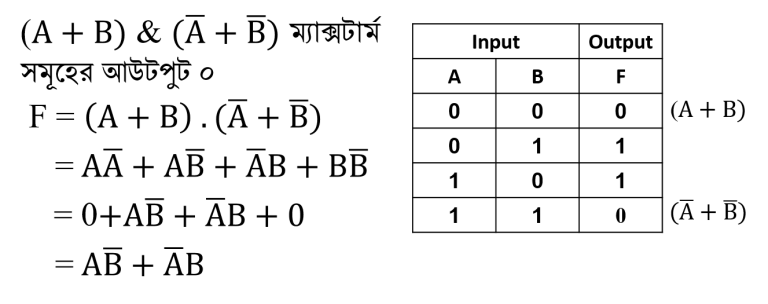
সত্যক সারণিতে ব্যবহৃত ইনপুট বিন্যাসসমূহের যোগফলকে বলা হয় ম্যাক্সটার্ম। প্রতিটি ম্যাক্সটার্মের মান ০ হয়। সত্যক সারণির যেসব ম্যাক্সটার্মের আউটপুট মান ০, সেই ম্যাক্সটার্মসমূহ গুণ করে আউটপুট ফাংশন বা সমীকরণ নির্ণয় করা হয়। এ পদ্ধতিকে POS (Product of Sums) বলা হয়।
অর্থাৎ উভয় প্রক্রিয়ায় একই বুলিয়ান ফাংশন পাওয়ার যায়।
সত্যক সারণির সাহায্যে বুলিয়ান সমীকরন বা উপপাদ্যের প্রমানঃ
সত্যক সারণির সাহায্যে বুলিয়ান সমীকরণ প্রমাণের জন্য নিমোক্ত ধাপসমূহ অনুসরণ করা হয়-
১। বুলিয়ান সমীকরণটিতে ব্যবহৃত মোট চলক সংখ্যা নির্ণয় করতে হয়। n সংখ্যক চলকের জন্য সত্যক সারণিতে ২n সংখ্যক ভিন্ন ভিন্ন ইনপুট সেট হয়।
২। সত্যক সারণির মূল কাঠামো তৈরির জন্য সমীকরণে যতোগুলো চলক আছে ততোগুলো কলাম এবং ২n সংখ্যক ভিন্ন ভিন্ন ইনপুট সেট দেওয়ার জন্য ২n সংখ্যক সারি বা রো তৈরি করতে হয়।
৩। সমীকরণের বামপক্ষ ও ডানপক্ষ সমান প্রমাণের জন্য বামপক্ষ ও ডানপক্ষের সকল প্রোডাক্ট টার্ম নির্নয় করতে হয়।প্রোডাক্ট টার্ম নির্নয় করার জন্য প্রয়োজনীয় সাব-প্রোডাক্ট টার্ম নির্নয় করতে হয়। এক্ষেত্রে বিভিন্ন সাব-প্রোডাক্ট টার্ম বা প্রোডাক্ট টার্ম নির্নয়ের জন্য অতিরিক্ত কলাম তৈরি করতে হয়।
A ও B দুইটি চলকের জন্য ডি মরগ্যানের উপপাদ্য দুটি সত্যক সারণির সাহায্যে প্রমাণঃ
A , B ও C তিনটি চলকের জন্য ডি মরগ্যানের উপপাদ্যের প্রমাণঃ
