বুলিয়ান অ্যালজেবরা (Boolean algebra)
বুলিয়ান অ্যালজেবরা (Boolean algebra): বুলিয়ান অ্যালজেবরার উদ্ভাবক হলেন প্রখ্যাত ইংরেজ গণিতবিদ জর্জ বুল। জর্জ বুল সর্বপ্রথম গণিত ও যুক্তির মধ্যে সম্পর্ক আবিষ্কার করেন এবং গণিত ও যুক্তির ওপর ভিত্তি করে এক ধরণের অ্যালজেবরা তৈরি করেন, যাকে বুলিয়ান অ্যালজেবরা বলা হয়।
বুলিয়ান অ্যালজেবরা মূলত লজিকের সত্য অথবা মিথ্যা এ দুটি স্তরের উপর ভিত্তি করে তৈরি করা হয়েছে। অপরদিকে সকল ডিজিটাল ডিভাইস বাইনারি পদ্ধতিতে কাজ করে। এই ডিজিটাল ডিভাইসে গাণিতিক ও যুক্তিমূলক কাজ করার জন্য বুলিয়ান অ্যালজেবরা ব্যবহৃত হয়।
বুলিয়ান অ্যালজেবরার সত্য ও মিথ্যাকে যথাক্রমে বাইনারি “১“এবং “০” দ্বারা পরিবর্তন করে ডিজিটাল ডিভাইসের সকল গাণিতিক সমস্যা বুলিয়ান অ্যালজেবরার সাহায্যে সমাধান সম্ভব হয়।
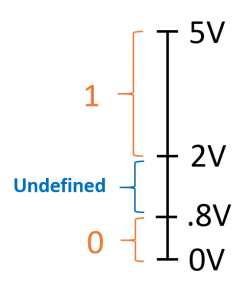
ডিজিটাল ডিভাইসে কোনো সার্কিটে বিদ্যুতের উপস্থিতিকে ১ ধরা হয় এবং বিদ্যুতের অনুপস্থিতিকে ০ ধরা হয়। ডিজিটাল সিস্টেমে ভোল্টেজ লেভেল ০ থেকে .৮ ভোল্টকে লজিক ০ ধরা হয় এবং ভোল্টেজ লেভেল ২ থেকে ৫ ভোল্টকে লজিক ১ ধরা হয়। ডিজিটাল সিস্টেমে +০.৮ ভোল্ট থেকে +২ ভোল্ট লেভেল সংজ্ঞায়িত নয় বিধায় ব্যবহার করা হয় না।
বুলিয়ান অ্যালজেবরার বৈশিষ্ট্যঃ
- বুলিয়ান অ্যালজেবরায় মাত্র দুটি অঙ্ক ‘০’ এবং ‘১’ ব্যবহৃত হয়।
- বুলিয়ান চলকের দুটি মান থাকায় বুলিয়ান অ্যালজেবরা দশমিক অ্যালজেবরার তুলনায় অনেক সহজ পদ্ধতি।
- বুলিয়ান অ্যালজেবরায় কোনো ভগ্নাংশ, লগারিদম, বর্গ, ঋণাত্মক সংখ্যা, কাল্পনিক সংখ্যা ইত্যাদি ব্যবহার করা যায় না।
- বুলিয়ান অ্যালজেবরায় শুধু মাত্র যৌক্তিক যোগ, গুণ ওপূরকের মাধ্যমে সমস্ত গাণিতিক কাজ করা হয়।
- বুলিয়ান অ্যালজেবরায় কোনো ধরনের জ্যামিতিক বা ত্রিকোণমিতিক সূত্র ব্যবহার করা যায় না।
বুলিয়ান অ্যালজেবরার ভিত্তিঃ
বুলিয়ান অ্যালজেবরা মূলত লজিকের সত্য অথবা মিথ্যা এ দুটি স্তরের উপর ভিত্তি করে তৈরি করা হয়েছে। অপরদিকে সকল ডিজিটাল ডিভাইস বাইনারি পদ্ধতিতে কাজ করে। এই ডিজিটাল ডিভাইসে গাণিতিক ও যুক্তিমূলক কাজ করার জন্য বুলিয়ান অ্যালজেবরা ব্যবহৃত হয়।
প্রতীক বা মৌলিক চিহ্নঃ দুটি – TRUE/ON/1 এবং FALSE/OFF/0
বুলিয়ান অ্যালজেবরার অপারেটরঃ
অপারেটরঃ ৩টি- AND ( . ), OR ( + ), NOT( ¯ )
বুলিয়ান অ্যালজেবরার মৌলিক অপারেশনঃ
বুলিয়ান অ্যালজেবরার মৌলিক অপারেশন ৩টি। যথা –
- অ্যান্ড অপারেশন (AND Operation) বা যৌক্তিক গুণ (Logical Multiplication)
- অর অপারেশন (OR Operation) বা যৌক্তিক যোগ (Logical Addition)
- নট অপারেশন (NOT Operation) বা যৌক্তিক পূরক (Logical Inversion)
বুলিয়ান অ্যালজেবরার সূত্রঃ
বুলিয়ান উপাপাদ্য, ডি-মরগ্যান উপাপাদ্য, দ্বৈতনীতি ইত্যাদি
বুলিয়ান চলকঃ
বুলিয়ান অ্যালজেবরায় যে রাশির মান পরিবর্তনশীল তাকে বুলিয়ান চলক বলে। যেমন- Y = A+ 0 + 1, এখানে A হচ্ছে চলক ।
বুলিয়ান ধ্রুবকঃ
বুলিয়ান অ্যালজেবরায় যে রাশির মান অপরিবর্তনশীল থাকে তাকে বুলিয়ান ধ্রুবক বলে। যেমন- Y = A+ 0 + 1, এখানে 0 এবং 1 হচ্ছে বুলিয়ান ধ্রুবক।
ধ্রুবকের মান সব সময় অপরিবর্তিত থাকে কিন্তু চলকের মান পরিবর্তিত হয়। বিভিন্ন ইলেকট্রনিক বর্তনীর ইনপুট ও আউটপুটের লজিক অবস্থা নির্দিষ্ট করার জন্য বুলিয়ান চলক ও ধ্রুবক ব্যবহার করা হয়।
বুলিয়ান পূরকঃ
বুলিয়ান অ্যালজেবরায় যেকোনো চলকের মান ০ অথবা ১ হয়। এই ০ এবং ১ কে একটি অপরটির বুলিয়ান পূরক বলা হয়। বুলিয়ান পূরকে ‘–’ চিহ্নের মাধ্যমে প্রকাশ করা হয়। গণিতের ভাষায় লেখা হয় A এর পূরক A′।
বুলিয়ান স্বতঃসিদ্ধ
বুলিয়ান অ্যালজেবরায় সমস্ত গাণিতিক কাজ শুধুমাত্র যৌক্তিক যোগ, গুণ ও পূরকের সাহায্যে করা হয়। বুলিয়ান অ্যালজেবরায় যৌক্তিক যোগ, গুণ ও পূরকের নিয়মগুলোকে বুলিয়ান স্বতঃসিদ্ধ বলে। বুলিয়ান স্বতঃসিদ্ধ গুলো-
- যোগের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of OR)
- গুণের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of AND)
- পূরকের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of NOT)
যোগের বুলিয়ান স্বতঃসিদ্ধঃ
যৌক্তিক যোগের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে যোগের বুলিয়ান স্বতঃসিদ্ধ বলে। যৌক্তিক যোগের সময় বুলিয়ান চলকগুলোর মানের মধ্যে OR(+) অপারেটর ব্যবহার করা হয় তা প্রচলিত যোগের চিহ্ন নয়। বুলিয়ান অ্যালজেবরায় এ যোগ চিহ্নকে যৌক্তিক যোগ হিসেবে ব্যবহার করা হয়। যৌক্তিক যোগের চারটি নিয়ম প্রচলিত। যথা−
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
উপরের বুলিয়ান স্বতঃসিদ্ধ থেকে বলা যায় যে, বুলিয়ান অ্যালজেবরায় যৌক্তিক যোগের ক্ষেত্রে যেকোনো একটির মান ১ হলে যৌক্তিক যোগফল ১ হবে, অন্যথায় ০ হবে।
গুণের বুলিয়ান স্বতঃসিদ্ধঃ
যৌক্তিক গুণের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে গুণের বুলিয়ান স্বতঃসিদ্ধ বলে। যৌক্তিক গুণের সময় বুলিয়ান চলকগুলোর মানের মধ্যে AND(.) অপারেট ব্যবহার করা হয়। যৌক্তিক গুণের চারটি নিয়ম প্রচলিত। যথা:
0 . 0 = 0
0 . 1 = 0
1 . 0 = 0
1 . 1 = 1
উপরের বুলিয়ান স্বতঃসিদ্ধ থেকে বলা যায় যে, বুলিয়ান অ্যালজেবরায় যৌক্তিক গুণের ক্ষেত্রে যেকোনো একটির মান ০ হলে যৌক্তিক গুণফল ০ হবে, অন্যথায় ১ হবে।
পূরকের বুলিয়ান স্বতঃসিদ্ধঃ
যৌক্তিক পূরকের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে পূরকের বুলিয়ান স্বতঃসিদ্ধ বলে। যৌক্তিক পূরকের সময় বুলিয়ান চলকগুলোর উপর পূরক চিহ্ন ( ¯ ) ব্যবহার করা হয়। বুলিয়ান অ্যালজেবরায় যৌক্তিক পূরকের ক্ষেত্রে ০ থাকলে ১ হয়, এবং ১ থাকলে ০ হয়।
1´ = 0
0´ = 1
বুলিয়ান দ্বৈতনীতিঃ
বুলিয়ান অ্যালজেবরায় ব্যবহৃত সকল উপপাদ্য বা সমীকরণ যে দুটি নিয়ম মেনে একটি বৈধ্য সমীকরণ থেকে অপর একটি বৈধ্য সমীকরণ নির্ণয় করা যায় তাকে বুলিয়ান দ্বৈতনীতি বলে। অর্থাৎ বুলিয়ান অ্যালজেবরায় অর (OR) এবং অ্যান্ড (AND) এর সাথে সম্পর্কযুক্ত সকল উপপাদ্য বা সমীকরণ দ্বৈতনীতি মেনে চলে। এ নিয়ম দু টি হলো −
১। ০ এবং ১ পরস্পর বিনিময় করে অর্থাৎ ০ এর পরিবর্তে ১ এবং ১ এর পরিবর্তে ০ ব্যবহার করে।
২। অর (+) এবং অ্যান্ড (.) পরস্পর বিনিময় করে অর্থাৎ অর (+) এর পরিবর্তে অ্যান্ড (.) এবং অ্যান্ড (.) এর পরিবর্তে অর (+) ব্যবহার করে।
উদাহরণ: ১ + ১ = ১ সমীকরণে ১ এর পরিবর্তে ০ এবং (+) এর পরিবর্তে (.) বসিয়ে পাই ০.০ = ০ এটাও একটি বৈধ্য সমীকরণ। আবার ০.১ = ০ সমীকরণে ০ এর পরিবর্তে ১ ও ১ এর পরিবর্তে ০ এবং (.) এর পরিবর্তে (+) বসিয়ে পাই ১ + ০ =১ এটাও একটি বৈধ্য সমীকরণ।
বুলিয়ান উপপাদ্য
১৯৪০ সালে E.V Huntington বুলিয়ান অ্যালজেবরার জন্য কিছু উপপাদ্য তৈরি করেন, যার সাহায্যে বুলিয়ান অ্যালজেবরার জটিল সমীকরণকে সরলীকরণ করা যায়। এই উপপাদ্যগুলোকে হানটিংটন উপপাদ্য বলা হয়।
বুলিয়ান অ্যালজেবরার মৌলিক উপপাদ্য (Basic Theorem):
বুলিয়ান যোগের ক্ষেত্রে মৌলিক উপপাদ্যসমূহের প্রমানঃ
বুলিয়ান গুণের ক্ষেত্রে মৌলিক উপপাদ্যসমূহের প্রমানঃ
মৌলিক উপপাদ্য ছাড়াও বিভিন্ন উপপাদ্য ব্যবহৃত হয়। যেমন –