পাঠ-১: সংখ্যা পদ্ধতির (Number System) ধারণা ও এর প্রকারভেদ

সংখ্যা পদ্ধতি (Number System)

সংখ্যা পদ্ধতিঃ কোনো সংখ্যাকে লিখা বা প্রকাশ ও এর সাহায্যে গাণিতিক হিসাব-নিকাশের জন্য ব্যবহৃত পদ্ধতিই হলো সংখ্যা পদ্ধতি (Number System)।

সংখ্যা আবিষ্কারের ইতিহাসঃ সভ্যতার সূচনালগ্ন থেকেই মানুষ হিসাব-নিকাশের প্রয়োজনীয়তা অনুভব করে। তখন গণনার জন্য নানা রকম উপকরণ যেমন- হাতের আঙ্গুল, নুডি পাথর, কাঠি, ঝিনুক, রশির গিট, দেয়ালে দাগ কাটা ইত্যাদি ব্যবহার করা হতো। সময়ের বিবর্তনে গণনার ক্ষেত্রে বিভিন্ন চিহ্ন ও প্রতীক ব্যবহার শুরু হতে থাকে। খ্রিস্টপূর্ব ৩৪০০ সালে হায়ারোগ্লিফিক্স সংখ্যা পদ্ধতির মাধ্যমে সর্বপ্রথম গণনার ক্ষেত্রে লিখিত সংখ্যা বা চিহ্নের ব্যবহার শুরু হয়। পরবর্তিতে পর্যায়ক্রমে মেয়ান,  রোমান ও দশমিক সংখ্যা পদ্ধতির ব্যবহার শুরু হয়।

সংখ্যাঃ সংখ্যা হচ্ছে এমন একটি উপাদান যা কোনকিছু গণনা, পরিমাণ এবং পরিমাপ করার জন্য ব্যবহৃত হয়। যেমন- একাদশ শ্রেণীতে ২৪৩ জন ছাত্র আছে; এখানে ২৪৩ একটি সংখ্যা।

অংকঃ সংখ্যা তৈরির ক্ষুদ্রতম প্রতীকই হচ্ছে অংক। সকল অংক সংখ্যা কিন্তু সকল সংখ্যা অংক নয়। যেমন ২৪৩ তিন অংক বিশিষ্ট একটি সংখ্যা ,যা ২, ৪ এবং ৩ পৃথক তিনটি অংক নিয়ে গঠিত। যারা প্রত্যেকেই পৃথকভাবে একেকটি সংখ্যা।

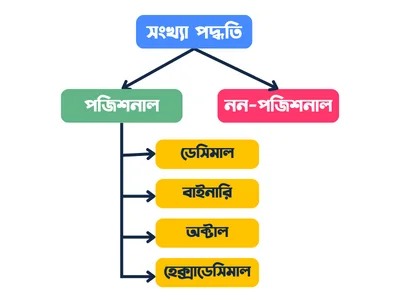
অবস্থানের উপর ভিত্তি করে বা শুরু থেকে আজ পর্যন্ত সৃষ্ট সংখ্যা পদ্ধতিকে প্রধানত দুইভাগে ভাগ করা হয়। যথা:

১। নন-পজিশনাল (অস্থানিক) সংখ্যা পদ্ধতি

২। পজিশনাল (স্থানিক) সংখ্যা পদ্ধতি

ICT অধ্যায় ভিত্তিক নোট ডাউনলোড করতে ক্লিক করো

নন-পজিশনাল সংখ্যা পদ্ধতিঃ

যে সংখ্যা পদ্ধতিতে সংখ্যার মান সংখ্যায় ব্যবহৃত অংকসমূহের অবস্থানের উপর নির্ভর করে না তাকে নন-পজিশনাল সংখ্যা পদ্ধতি বলে। এই পদ্ধতিতে বিভিন্ন চিহ্ন বা প্রতীকের মাধ্যমে হিসাব-নিকাশের কাজ করা হতো । এই পদ্ধতিতে ব্যবহৃত প্রতীক বা অংকগুলোর পজিশন বা অবস্থান গুরত্ব পায় না। ফলে অংকগুলোর কোনো স্থানীয় মান থাকে না। শুধু অংকটির নিজস্ব মানের উপর ভিত্তি করে হিসাব-নিকাশ কার হয়। প্রাচীন কালে ব্যবহৃত হায়ারোগ্লিফিক্স (Hieroglyphics), মেয়ান ও রোমান, ট্যালি সংখ্যা পদ্ধতি নন-পজিশনাল সংখ্যা পদ্ধতির উদাহরণ।

পজিশনাল সংখ্যা পদ্ধতিঃ

যে সংখ্যা পদ্ধতিতে সংখ্যার মান সংখ্যায় ব্যবহৃত অংকসমূহের পজিশন বা অবস্থানের উপর নির্ভর করে তাকে পজিশনাল সংখ্যা পদ্ধতি  বলে। এই সংখ্যা পদ্ধতিতে সংখ্যায় ব্যবহৃত অংকসমূহের নিজস্ব মান, স্থানীয় মান এবং সংখ্যা পদ্ধতির ভিত্তির সাহায্যে সংখ্যার মান নির্ণয় করা হয়। এই সংখ্যা পদ্ধতিতে Radix point(.) দিয়ে প্রতিটি সংখ্যাকে পূর্ণাংশ এবং ভগ্নাংশ এই দুইভাগে বিভক্ত করা হয়। যেমনঃ (১২৬.৩৪)১০

কোন সংখ্যা পদ্ধতিতে একটি সংখ্যায় কোন অঙ্কের স্থানীয় মান হল (সংখ্যাটির বেজ) অঙ্কের পজিশন। পজিশনাল সংখ্যা পদ্ধতিতে কোন সংখ্যার পূর্নাংশের অংকগুলোর পজিশন শুরু হয় ০ থেকে(ডান থেকে বাম দিকে) এবং ভগ্নাংশের অংকগুলোর পজিশন শুরু হয় -১ থেকে(বাম থেকে ডান দিকে)।  যেমন (১২৬.৩৪)১০ সংখ্যাটির ২ অঙ্কটির স্থানীয় মান হল (১০)১= ১০ এবং ১ অঙ্কটির স্থানীয় মান হল (১০)২= ১০০। পজিশনাল সংখ্যা পদ্ধতিতে একটি সংখ্যার বিভিন্ন অংশ:

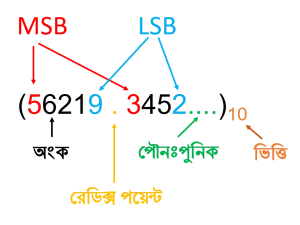
পজিশনাল সংখ্যা পদ্ধতি চার প্রকার। যথা-

১) বাইনারি

২) অক্টাল

৩) ডেসিমেল

৪) হেক্সাডেসিমেল

ICT অধ্যায় ভিত্তিক নোট ডাউনলোড করতে ক্লিক করো

বাইনারি সংখ্যা পদ্ধতিঃ

Bi শব্দের অর্থ হলো ২ (দুই)। যে সংখ্যা পদ্ধতিতে ০  ও ১ এই দুইটি প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে বাইনারি সংখ্যা পদ্ধতি বলে। যেমন-(১০১০)২। বাইনারি সংখ্যা পদ্ধতিতে যেহেতু ০ এবং ১ এই দুইটি প্রতিক বা চিহ্ন ব্যবহার করা হয় তাই এর বেজ বা ভিত্তি হচ্ছে ২। ইংল্যান্ডের গণিতবিদ জর্জ বুল বাইনারি সংখ্যা পদ্ধতি উদ্ধাবন করেন। বাইনারি সংখ্যা পদ্ধতি সবচেয়ে সরলতম সংখ্যা পদ্ধতি। বাইনারি সংখ্যা পদ্ধতির ০ এবং ১ এই দুটি মৌলিক চিহ্নকে বিট বলে এবং আট বিটের গ্রুপ নিয়ে গঠিত হয় একটি বাইট।

সকল ইলেক্ট্রনিক্স ডিভাইস শুধুমাত্র দুটি অবস্থা অর্থাৎ বিদ্যুতের উপস্থিতি এবং অনুপস্থিতি বুজতে পারে। বিদ্যুতের উপস্থিতিকে ON, HIGH, TRUE কিংবা YES বলা হয় যা লজিক লেভেল ১ নির্দেশ করে এবং বিদ্যুতের অনুপস্থিতিকে OFF, LOW, FALSE কিংবা NO বলা হয় যা লজিক লেভেল ০ নির্দেশ করে। লজিক লেভেল ০ এবং ১ বাইনারি সংখ্যা পদ্ধতির সাথে সামঞ্জন্যপূর্ণ। তাই কম্পিউটার বা সকল ইলেক্ট্রনিক্স ডিভাইসে বাইনারি সংখ্যা পদ্ধতি ব্যবহৃত হয়।

অক্টাল সংখ্যা পদ্ধতিঃ

Octa শব্দের অর্থ হলো ৮ । যে সংখ্যা পদ্ধতিতে ৮টি (০,১,২,৩,৪,৫,৬,৭) প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে অকটাল সংখ্যা পদ্ধতি বলে। যেমন- (১২০)৮ । অকটাল সংখ্যা পদ্ধতিতে ০ থেকে ৭ পর্যন্ত মোট ৮ টি প্রতিক বা চিহ্ন নিয়ে যাবতীয় গাণিতিক কর্মকান্ড সম্পাদন করা হয় বলে এর বেজ বা ভিত্তি হলো ৮। অক্টাল সংখ্যা পদ্ধতিকে তিন বিট সংখ্যা পদ্ধতিও বলা হয়। কারণ অকটাল সংখ্যা পদ্ধতিতে ব্যবহৃত ০ থেকে ৭ পর্যন্ত মোট ৮ টি প্রতিক বা চিহ্নকে তিন বিটের মাধ্যমেই প্রকাশ করা যায়। ডিজিটাল সিস্টেমে বিভিন্ন ক্ষেত্রে বাইনারি সংখ্যাকে নির্ভূল ও সহজে উপস্থাপন করার জন্য অক্টাল সংখ্যা পদ্ধতি ব্যবহার করা হয়।

ডেসিমেল সংখ্যা পদ্ধতিঃ

Deci শব্দের অর্থ হলো ১০। যে সংখ্যা পদ্ধতিতে ১০টি (০,১,২,৩,৪,৫,৬,৭,৮,৯) প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে ডেসিমেল বা দশমিক সংখ্যা পদ্ধতি বলে।যেমন- (১২০)১০ ।  দশমিক সংখ্যা পদ্ধতিতে ০ থেকে ৯ পর্যন্ত মোট ১০ টি প্রতিক বা চিহ্ন ব্যবহার করা হয় বলে এর বেজ বা ভিত্তি হচ্ছে ১০। ইউরোপে আরোবরা এই সংখ্যা পদ্ধতির প্রচলন করায় অনেকে এটিকে আরবি সংখ্যা পদ্ধতি নামেও অভিহিত করেন। মানুষ সাধারণত গণনার কাজে ডেসিমেল সংখ্যা পদ্ধতি ব্যবহার করে।

হেক্সাডেসিমেল সংখ্যা পদ্ধতিঃ

হেক্সাডেসিমেল শব্দটির দুটি অংশ। একটি হলো হেক্সা(Hexa) অর্থাৎ ৬ এবং অপরটি ডেসিমেল অর্থাৎ ১০ , দুটো মিলে হলো ষোল। যে সংখ্যা পদ্ধতিতে ১৬ টি (০,১,২,৩,৪,৫,৬,৭,৮,৯,A,B,C,D,E,F) প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে হেক্সাডেসিমেল সংখ্যা পদ্ধতি বলে। যেমন- (১২০৯A)১৬। হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে মোট ১৬ টি প্রতিক বা চিহ্ন ব্যবহার করা হয় বলে এর বেজ বা ভিত্তি হচ্ছে ১৬। হেক্সাডেসিমেল সংখ্যা পদ্ধতিকে চার বিট সংখ্যা পদ্ধতিও বলা হয়। কারণ হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে ব্যবহৃত ১৬ টি (০,১,২,৩,৪,৫,৬,৭,৮,৯,A,B,C,D,E,F) প্রতিক বা চিহ্নকে চার বিটের মাধ্যমেই প্রকাশ করা যায়।  ডিজিটাল সিস্টেমে বিভিন্ন ক্ষেত্রে বাইনারি সংখ্যাকে নির্ভূল ও সহজে উপস্থাপন করার জন্য হেক্সাডেসিমেল সংখ্যা পদ্ধতি ব্যবহার করা হয়। এছাড়া বিভিন্ন মেমোরি অ্যাড্রেস ও রং এর কোড হিসেবে হেক্সাডেসিমেল সংখ্যা পদ্ধতি ব্যবহার করা হয়।

ICT অধ্যায় ভিত্তিক নোট ডাউনলোড করতে ক্লিক করো

সংখ্যা পদ্ধতির বেজঃ

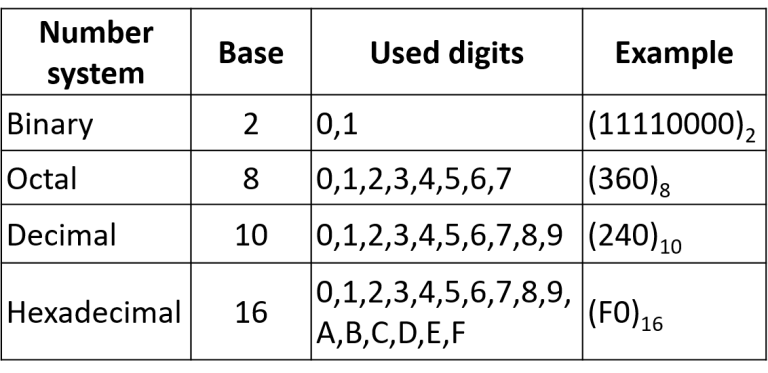
কোনো একটি সংখ্যা পদ্ধতিতে ব্যবহৃত মৌলিক চিহ্নসমূহের মোট সংখ্যা বা সমষ্টিকে ঐ সংখ্যা পদ্ধতির বেজ (Base) বা ভিত্তি বলে। কোন একটি সংখ্যা কোন সংখ্যা পদ্ধতিতে লেখা তা বুঝানোর জন্য সংখ্যার সাথে বেজ বা ভিত্তিকে সাবস্ক্রিপ্ট (সংখ্যার ডানে একটু নিচে) হিসেবে লিখে প্রকাশ করা হয়। যেমন-

• বাইনারি ১০১০ কে (১০১০)_২
• অক্টাল ১২০ কে (১২০)_৮
• ডেসিম্যাল ১২০ কে (১২০)_১০
• হেক্সাডেসিম্যাল ১২০ কে (১২০)_১৬

 

সংখ্যার স্থানীয় মান নির্ণয়

 

কোন ডিজিটের স্থানীয় মান = (সংখ্যার বেজ)^{ডিজিট পজিশন}

উদাহরনঃ (2345.012)₁₀  এর মধ্যে ৩ এবং দশমিক সংখ্যা ২ এর স্থানীয় মান বের কর।

[ পূর্ন সংখ্যার ক্ষেত্রে ডিজিট পজিশন শুরু হয় ০ থেকে (ডান থেকে বাম দিকে) এবং ভগ্নাংশের ক্ষেত্রে ডিজিট পজিশন শুরু হয় -১ থেকে (বাম থেকে ডান দিকে)]

 

ICT অধ্যায় ভিত্তিক নোট ডাউনলোড করতে ক্লিক করো

জ্ঞানমূলক প্রশ্নসমূহঃ

ক। নম্বর (সংখ্যা) কি?

ক। ডিজিট (অংক) কি?

ক। সংখ্যা পদ্ধতি কী?

ক। পজিশনাল সংখ্যা পদ্ধতি কী?

ক। নন-পজিশনাল সংখ্যা পদ্ধতি কী?

ক। স্থানীয় মান কী?

ক। রেডিক্স পয়েন্ট কী?

ক। বাইনারি সংখ্যা পদ্ধতি কী?

ক। বিট/বাইট কী?

ক। অক্টাল সংখ্যা পদ্ধতি কী?

ক। ডেসিমেল সংখ্যা পদ্ধতি কী?

ক। হেক্সাডেসিমেল সংখ্যা পদ্ধতি কী?

ক। সংখ্যা পদ্ধতির বেজ বা ভিত্তি কী?

জ্ঞানমূলক প্রশ্নের উত্তর উত্তর জানতে ক্লিক কর

অনুধাবনমূলক প্রশ্নসমূহঃ

খ। “সকল অংকই সংখ্যা কিন্তু সকল সংখ্যা অংক নয়”- ব্যাখ্যা কর।

খ। “ট্যালি একটি ননপজিশনাল সংখ্যা পদ্ধতি”- ব্যাখ্যা কর।

খ। সংখ্যা পদ্ধতির বেজ ব্যাখ্যা কর।

খ। (১১)_১০  সংখ্যাটিকে পজিশনাল সংখ্যা বলা হয় কেন?

খ। সংখ্যা পদ্ধতিতে ১০১০১ কী ধরনের সংখ্যা বর্ণনা কর।

খ। ৯৮৮ সংখ্যাটি কোন ধরনের সংখ্যা পদ্ধতির- ব্যাখ্যা কর।

খ। 3D কোন ধরনের সংখ্যা? ব্যাখ্যা কর।

খ। ৩ ভিত্তিক সংখ্যা পদ্ধতি- ব্যাখ্যা কর।

খ। (২৯৮)_৮ সঠিক কিনা- ব্যাখ্যা কর।

খ। “কম্পিউটারের অভ্যন্তরীণ যন্ত্রাংশের কার্যপদ্ধতির সাথে বাইনারি সংখ্যা পদ্ধতি সামঞ্জস্যপূর্ণ”- ব্যাখ্যা কর।

খ। কম্পিউটারের ক্ষেত্রে ডিজিটাল সিগনাল উপযোগী কেন? ব্যাখ্যা কর।

খ। কম্পিউটার ডিজাইনে বাইনারি সংখ্যা পদ্ধতির ব্যবহারের কারণ লিখ।

খ। হেক্সাডেসিমেল ও দশমিক সংখ্যা পদ্ধতির মধ্যে তুমি কিভাবে পার্থক্য করবে?

খ। “অক্টাল তিন বিটের কোড”- বুঝিয়ে লিখ।

খ। “হেক্সাডেসিমেল চার বিটের কোড” – বুঝিয়ে লিখ।

অনুধাবন মূলক প্রশ্নের উত্তর জানতে ক্লিক কর