চিহ্নযুক্ত সংখ্যা – ১ ও ২ এর পরিপূরক (Signed Numbers)
চিহ্নযুক্ত সংখ্যা (Signed Numbers): যখন কোন সংখ্যার পূর্বে ধনাত্মক(+) বা ঋণাত্মক(-) চিহ্ন থাকে তখন সেই সংখ্যাকে চিহ্নযুক্ত সংখ্যা বা সাইনড নম্বর বলা হয়।
চিহ্ন বিটঃ বাইনারি পদ্ধতিতে চিহ্নযুক্ত সংখ্যা উপস্থাপনের জন্য প্রকৃত মানের পূর্বে একটি অতিরিক্ত বিট যোগ করা হয়। এ অতিরিক্ত বিটকে চিহ্ন বিট বলে। চিহ্ন বিট 0 হলে সংখ্যাটি ধনাত্মক এবং চিহ্নবিট ১ হলে সংখ্যাটিকে ঋণাত্মক ধরা হয়।
n বিটের একটি রেজিস্টার n বিটের বাইনারি তথ্য ধারণ করতে পারে। অর্থাৎ ৮-বিট রেজিস্টার, ১৬- বিট রেজিস্টার, ৩২-বিট রেজিস্টার ইত্যাদি যথাক্রমে ৮, ১৬, ৩২ বিট তথ্য ধারণ করতে পারে। অর্থাৎ n-bit রেজিস্টারের ক্ষেত্রে সর্বডানের n-1 বিট হল ডেটা বিট এবং সর্ব বামের বিটটি চিহ্ন বিট হিসেবে ব্যবহৃত হয়।
কখন কত বিট রেজিস্টার ব্যবহার করতে হবে তা নির্ভর করে প্রদত্ত সংখ্যার উপর। যদি একটি সংখ্যার ডেটা বিট ৭ বিটের বেশি হয় তখন ১৬ রেজিস্টার ব্যবহার করতে হবে এবং ডেটা বিট ১৫ বিটের বেশি হলে ৩২ রেজিস্টার ব্যবহার করতে হবে।
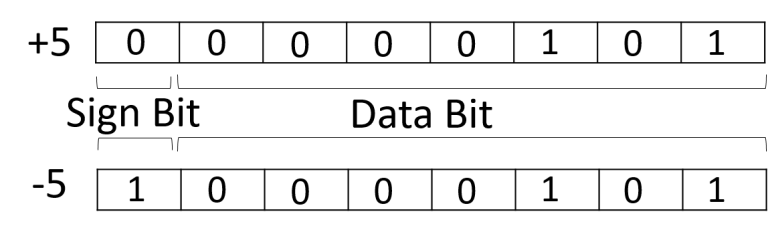
প্রকৃত মান গঠনঃ প্রকৃত মান গঠন প্রক্রিয়ায় +০ এবং -০ এর ভিন্ন ভিন্ন মান পাওয়া যায় যা বাস্তবের সাথে অসামঞ্জস্যপূর্ণ। প্রকৃত মান গঠন সহজ হলেও এর জন্য জটিল বর্তনীর প্রয়োজন হয়। প্রকৃত মান গঠন প্রক্রিয়ায় +5 এবং -5 কে ৮-বিট রেজিস্টারে উপস্থাপনঃ
যেহেতু ৮-বিট রেজিস্টার ব্যবহৃত হয়েছে, তাই ডেটা বিট ৭-বিট। কিন্তু ৫ এর ডেটা বিট ১০১ তিন বিট। তা বাকি গুলো ০ দ্বারা পূর্ন করা হয়েছে।
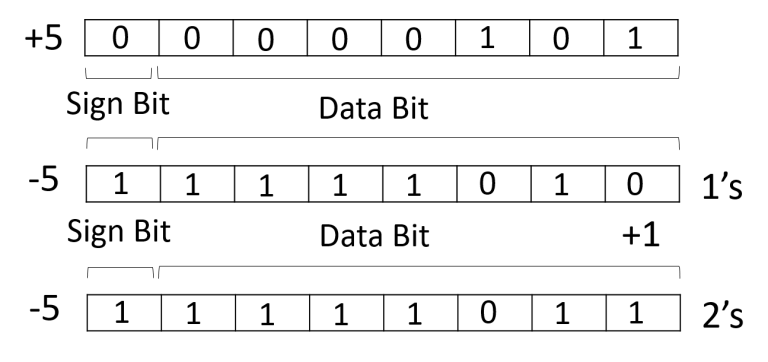
১ এর পরিপূরক গঠনঃ কোন বাইনারি সংখ্যার প্রতিটি বিটকে পূরক করে বা উল্টিয়ে যে সংখ্যা পাওয়া যায় তাকে ১ এর পরিপূরক বলা হয়। এই প্রক্রিয়ায় +০ এবং -০ এর ভিন্ন ভিন্ন মান পাওয়া যায় যা বাস্তবের সাথে অসামঞ্জস্যপূর্ণ।
যেহেতু ৮-বিট রেজিস্টার ব্যবহৃত হয়েছে, তাই ডেটা বিট ৭-বিট। কিন্তু ৫ এর ডেটা বিট ১০১ তিন বিট। তা বাকি গুলো ০ দ্বারা পূর্ন করা হয়েছে।
[ কোন ধনাত্মক (+) সংখ্যাকে ১ এর পরিপূরক করলে সংখাটি ঋণাত্মক (-) সংখ্যায় পরিনত হয়। আবার কোন ঋণাত্মক (-) সংখ্যাকে ১ এর পরিপূরক করলে সংখাটি ধনাত্মক (+) সংখ্যায় পরিনত হয়।]
২ এর পরিপূরক গঠনঃ কোন বাইনারি সংখ্যার ১ এর পরিপূরকের সাথে বাইনারি ১ যোগ করলে যে সংখ্যা পাওয়া যায় তাকে ২ এর পরিপূরক বলা হয়। ২ এর পরিপূরক গঠনে +০ এবং -০ এর মান একই যা বাস্তবের সাথে সামঞ্জস্যপূর্ণ। এই প্রক্রিয়ার বিভিন্ন সুবিধার কারণে ডিজিটাল ডিভাইসে ব্যপকভাবে ব্যবহৃত হচ্ছে।
যেহেতু ৮-বিট রেজিস্টার ব্যবহৃত হয়েছে, তাই ডেটা বিট ৭-বিট। কিন্তু ৫ এর ডেটা বিট ১০১ তিন বিট। তা বাকি গুলো ০ দ্বারা পূর্ন করা হয়েছে।
[ কোন ধনাত্মক (+) সংখ্যাকে ১ এর পরিপূরক করলে সংখাটি ঋণাত্মক (-) সংখ্যায় পরিনত হয়। আবার কোন ঋণাত্মক (-) সংখ্যাকে ১ এর পরিপূরক করলে সংখাটি ধনাত্মক (+) সংখ্যায় পরিনত হয়।]
২ এর পরিপূরক গঠনের গুরুত্ব:
১। প্রকৃত মান গঠন ও ১ এর পরিপূরক গঠনে +০ এবং -০ এর ভিন্ন ভিন্ন মান পাওয়া যায় যা বাস্তবের সাথে অসামঞ্জস্যপূর্ণ। কিন্তু ২ এর পরিপূরক গঠনে +০ এবং -০ এর মান একই যা বাস্তবের সাথে সামঞ্জস্যপূর্ণ।
২। ২ এর পরিপূরক গঠনে সরল বর্তনী প্রয়োজন যা দামে সস্তা এবং দ্রুত গতিতে কাজ করে।
৩। ২ এর পরিপূরক গঠনে চিহ্ন যুক্ত সংখ্যা এবং চিহ্নবিহীন সংখ্যা যোগ করার জন্য একই বর্তনী ব্যবহার করা যায়।
৪। ২ এর পরিপূরক গঠনে যোগ ও বিয়োগের জন্য একই বর্তনী ব্যবহার করা যায়। তাই আধুনিক কম্পিউটারে ২ এর পরিপূরক গঠন ব্যবহৃত হয়।
২ এর পরিপূরক পদ্ধতিতে যোগ:
১। প্রদত্ত চিহ্নযুক্ত সংখ্যা দুটির ২ এর পরিপূরক পদ্ধতিতে মান নির্নয় করতে হবে।
২। অতঃপর প্রাপ্ত মানের বাইনারি যোগ করতে হবে।
৩। যোগফলে অতিরিক্ত ক্যারি/বিট থাকলে তা বাদ দিতে হবে।
৪। এভাবে প্রাপ্ত সংখ্যাটিই হবে প্রদত্ত সংখ্যা দুটির যোগফল।
উদাহরন-১ঃ ৮-বিট রেজিস্টারের জন্য -২৫ এবং +১২ এর যোগফল নির্ণয়ঃ উদাহরন-২ঃ ৮-বিট রেজিস্টারের জন্য +২৫ এবং -১২ এর যোগফল নির্ণয়।
উদাহরন-২ঃ ৮-বিট রেজিস্টারের জন্য +২৫ এবং -১২ এর যোগফল নির্ণয়।
উদাহরন-৩ঃ ৮-বিট রেজিস্টারের জন্য -২৫ এবং -১২ এর যোগফল নির্ণয়।
উদাহরন-৪ঃ ৮-বিট রেজিস্টারের জন্য +২৫ এবং +১২ এর যোগফল নির্ণয়।
২ এর পরিপূরক পদ্ধতিতে বিয়োগ/যোগের মাধ্যমে পার্থক্য নির্ণয়
১। প্রদত্ত চিহ্নযুক্ত সংখ্যা দুটির মধ্যে যে সংখ্যাটি বিয়োগ করতে হবে তার চিহ্ন পরিবর্তন করে তার ২ এর পরিপূরক পদ্ধতিতে মান নির্নয় করতে হবে (অর্থাৎ +৫ থাকলে -৫ এর মান অথবা -৫ থাকলে +৫ এর মান নির্নয় করতে হবে)।
২। অপর চিহ্নযুক্ত সংখ্যাটির ২ এর পরিপূরক পদ্ধতিতে মান নির্নয় করতে হবে।
৩। অতঃপর প্রাপ্ত মানের বাইনারি যোগ করতে হবে (বিয়োগের ক্ষেত্রেও যোগ করতে হয়)।
৪। যোগফলে অতিরিক্ত ক্যারি বিট থাকলে তা বাদ দিতে হবে।
৫। এভাবে প্রাপ্ত সংখ্যাটিই হবে প্রদত্ত সংখ্যা দুটির বিয়োগফল।
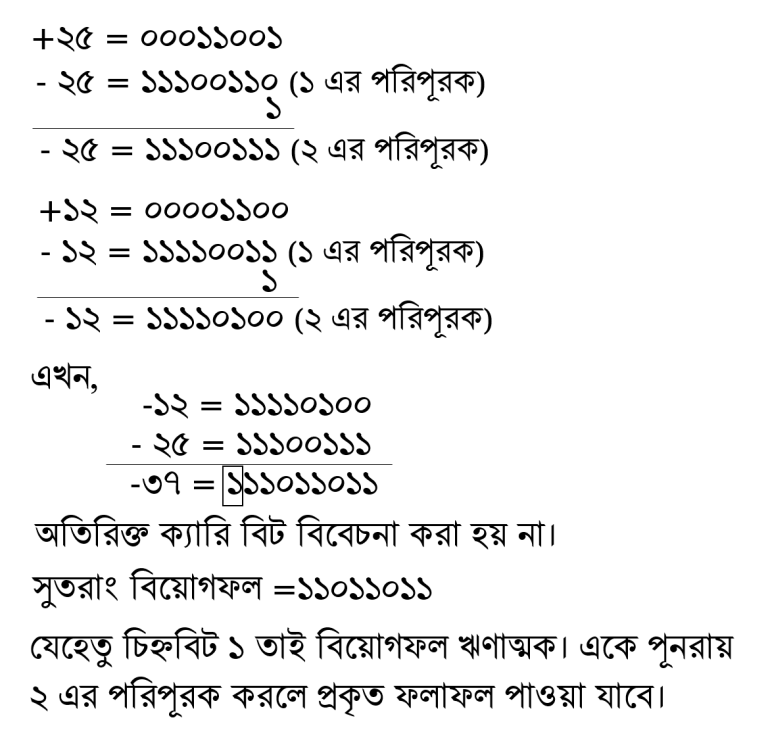
উদাহরন-১ঃ ৮-বিট রেজিস্টারের জন্য -২৫ এবং +১২ এর বিয়োগ নির্ণয়ঃ
= – ২৫ – ১২
= – ২৫ + (-১২)
উদাহরন-২ঃ ৮-বিট রেজিস্টারের জন্য +২৫ থেকে -১২ বিয়োগ কর।
উদাহরন-৩ঃ ৮-বিট রেজিস্টারের জন্য -২৫ থেকে -১২ বিয়োগ কর।
উদাহরন-৪ঃ ৮-বিট রেজিস্টারের জন্য +২৫ থেকে +১২ বিয়োগ কর।